Update

We concluded this research and decided to continue by building a cross-platform software solution where we leverage AI (Artificial Intelligence) and Deep Learning to accelerate CFD (Computational Fluid Dynamics) simulations. Learn more by visiting byteLAKE’s CFD Suite product website: www.byteLAKE.com/en/CFDSuite.

What is CFD?

CFD, Computational Fluid Dynamics tools combine numerical analysis and algorithms to solve fluid flows problems. They are used to model fluids density, velocity, pressure, temperature, and chemical concentrations in relation to time and space.

A range of industries such as automotive, chemical, aerospace, biomedical, power and energy, and construction rely on fast CFD analysis turnaround time. It is a key part of their design workflow to understand and design how liquids and gases flow and interact with surfaces.

Typical applications include weather simulations, aerodynamic characteristics modelling and optimization, and petroleum mass flow rate assessment.

Challenge: accelerate CFD simulations

CFD tools require a huge amount of computational power. The ever-increasing demand for accuracy and capabilities of the CFD workloads produces an exponential growth of the required computational resources. Their high algorithmic complexity maps naturally to the adaptable and reconfigurable Alveo platform, designed to dramatically accelerate time to insight on a broad range of challenging compute workloads in the Cloud and on-premise data centers.

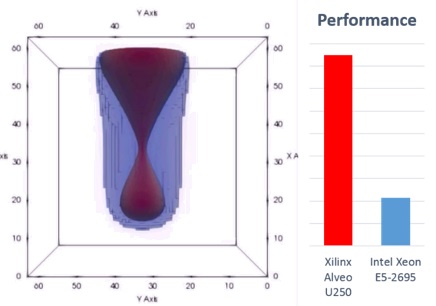
Moving to heterogeneous HPC (High Performance Computing) configurations powered by Xilinx Alveo helps significantly improve performance within radically reduced energy budgets.

Solution

byteLAKE has created a set of highly optimized CFD kernels that leverage the speed and energy efficiency of Xilinx Alveo accelerator cards powered by Xilinx UltraScale+ FPGAs to create a high-performance platform for complex engineering analysis.

Kernels can be directly adapted to the geophysical models such as EULAG (Eulerian/semi-Lagrangian) fluid solver, designed to simulate the all-scale geophysical flows. The algorithms have been extended by additional quantities as forces (implosion, explosion) and density vectors. In addition, they allow users to a fully configure the border conditions (periodic, open).

Key benefits

• Highly optimized CFD kernels for Xilinx® Alveo™ Datacenter accelerator cards
• 4x faster results
• 80% lower energy consumption
• Up to 6x better Performance per Watt
• Compatible with geophysical models like EULAG
• Fully configurable code
• Simpler, lower cost server infrastructure

CFD Kernels

• Advection
  – movement of some material (dissolved or suspended) in the fluid.
  
  As explained by Wikipedia, “advection is the transport of a substance or quantity by bulk motion. […] An example of advection is the transport of pollutants or silt in a river by bulk water flow downstream. […] The fluid’s motion is described mathematically as a vector field, and the transported material is described by a scalar field showing its distribution over space. […] In meteorology and physical oceanography, advection often refers to the transport of some property of the atmosphere or ocean, such as heat, humidity or salinity. Advection is important for the formation of orographic clouds and the precipitation of water from clouds, as part of the hydrological cycle.”
  
  Description:
  First-order step of the non-linear iterative upwind advection MPDATA (Multidimensional Positive Definite Advection Transport Algorithm) schemes. It belongs to the stencil group of algorithms that are used in i.e. Numerical Weather Prediction (NWP). It is based on forward-in-time techniques which are standard in computational meteorology, particularly in the context of semi-Lagrangian schemes.
• Pseudo Velocity
  – approximation of the relative velocity
  
  Description:
  Computation of the psuedo velocity for the second pass of upwind algorithm in MPDATA. This kernel is a key part of providing a second-order-accurate in non-linear advection schemes that suppress/reduce/control numerical oscillations characteristic of higher-order linear schemes.
• Divergence
  – measures how much of fluid is flowing into (negative divergence) or out (positive divergence) of a certain point in a vector field.
  Description:
  Divergence part of the matrix-free linear operator formulation in the iterative Krylov scheme. This algorithm is a part of linear systems via Krylov subspace methods. This method is widely used in variational data assimilation applications to NWP. Variational data assimilation is used at major weather prediction centers to produce the initial conditions for 7- to 10-days weather forecasts.
• Thomas algorithm
  – simplified form of Gaussian elimination for tridiagonal system of equations
  
  Description:
  Tridiagonal Thomas algorithm for vertical matrix inversion inside preconditioner for the iterative solver. Preconditioner operates on the diagonal part of the full linear problem. Effective preconditioning lies at the heart of multiscale flow simulation, including a broad range of geoscientific applications.

Find out more technical details in our blog post. Contact us at welcome@byteLAKE.com to get access to our highly optimized kernels for Xilinx® Alveo™ cards. These kernels can also be accessed through byteLAKE’s Alveo Products Marketplace.

Based on the result of this work and industry’s expectations for speedup and more efficient CFD solutions, byteLAKE made a strategic decision to invest in building a product named byteLAKE’s CFD Suite. Instead of adapting CFD solvers to accelerators, we use AI and work on a cross-platform solution to accelerate computations and enable new possibilities.